Spiiin's blog

1 - (2009) Python in imaginary world
2 - (2015) Scala in imaginary world
3 - (2021) Nim in imaginary world
4 - (2022) daScript in imaginery world
5 - (2023) AI in imaginery world
6 - (2024) F# in imaginery world

Потыкал несколько недель назад немного пазл из NES-игры James Bond Jr на C++ (выглядит так). Без особой цели, посмотреть на разные хеш-мапы в профайлере Visual Studio и в Tracy.

Исходники, quick & dirty, местами скорее всего с ошибками в предположениях и замерах. Возможно, когда-нибудь приведу в порядок и расставлю больше ссылок.

Наивное переписывание самый первой версии на Python с помощью chatgpt дало как-то работающее решение, находящее путь за несколько десятков шагов. В ходе исследований задачи на других языках я заранее знал (см. ссылку 5), что оптимальное число шагов - не больше 8, так что чтобы прийти к нему и перепроверить, что нет более коротких решений, отключил отбрасывание решений с плохой оценкой и включил честный поиск в ширину.

100 sec#

Наивная версия работает порядка 100 секунд и использует 3-3.5 гб памяти под словари. Её естественно захотелось поразгонять.

10 sec#

Для начала, взять нормальные структуры данных, можно использовать std::priority_map и хеш-таблицу с открытой адресацией ska::flat_hash_map.

• Хеш-таблицы. Шпаргалка — про то, почему таблицы с отрытой адресацией быстрее.
  ska::flat_hash_map содержит еще пачку оптимизаций и настроек, про которые будет ниже.

//When choosing a container, remember vector is best. Leave a comment to explain if you choose from the rest (c) Tony van Eerd
using OpenList = std::priority_queue<Node, std::vector<Node>, std::greater<Node>>;
using OpenHash = ska::flat_hash_map<size_t, uint8_t>;

С очередью вместо списка/массива решение занимает 60 сек, с таблицей с открытой адресацией вместо unordered_map сокращается - 18 сек.

На всех этапах я также периодически тыкал решения, которые заведомо не дадут ускорения, чтобы пощупать их относительные замедления.

boost::concurrent_flat_map — boost::concurrent_flat_map хеш-таблица с поддержкой многопоточности, в один поток - 24 сек. Хуже, потому что требует синхронизации на добавлениях.

Раскрытие вершин с помощью std::transform + разных std::execution политик - 44 сек. Требует времени на синхронизацию результатов после раскрытия.

Хранить не хеш вершин, а считать индекс перестановки относительно лексикографически отсортированной вершины (в исходниках с "bad_permutation") — прикидываем количество перестановок, и обращаемся не словарю, а к массиву на 25 млн элементов по индексу. Сам себе рассчёт номера перестановки — медленная операция (совсем медленно через генерацию самой перестановки std::next_permutation, быстрее по формулам, но особо не ускоришь дальше). Так что я попробовал использовать Zmeya для того, чтобы сохранить таблицу на диск и быстро её десериализовать. Библиотеки использует relative pointers — хранит индексы относительно базового адреса, так что позволяет десериализоваться без необходимости править эти индексы. При этом получается всё равно медленнее хеш-таблицы из-за долгого пересчёта вершины в её индекс. Снова около 100 сек, кажется.

constexpr unsigned long long factorial[] = { 1ULL, 1ULL, 2ULL, 6ULL, 24ULL, 120ULL, 720ULL, 5040ULL, 40320ULL, 362880ULL, 3628800ULL, 39916800ULL, 479001600ULL, 6227020800ULL, 87178291200ULL, 1307674368000ULL, 20922789888000ULL };

constexpr PackedMatrix permutationIndex(const Matrix& arr) {
    unsigned long long rank = 0;
    std::array<char, 4> freqs{ 2, 4, 4, 6 };
    for (std::size_t n = 0; n < arr.size(); ++n) {
        unsigned long long fsum = 0;
        int arrn = arr[n];
        for (int i = 0; i < arrn; ++i) {
            fsum += freqs[i];
        }
        unsigned long long fprod = 1;
        for (int freqIndex = 0u; freqIndex < freqs.size(); freqIndex++) {
            int freq = freqs[freqIndex];
            if (freq > 1) {
                fprod *= factorial[freq];
            }
        }

        rank += (fsum * factorial[arr.size() - n - 1]) / fprod;
        --freqs[arrn];
    }
    return static_cast<PackedMatrix>(rank);
}

Тут можно прочувствовать, что поиск элементов в хеш-таблице по сути состоит из 3х частей — преобразование элемента в его хеш/индекс + поиск индекса в коллекции + разрешение коллизии. Про первую часть реже говорят подробнее, на следующих шагах оптимизации будет важна и она. Но можно споткнуться об это и тут при беглой прикидке “поиск по индексу в массиве VS поиск по хеш-таблице, в которой могут быть коллизии”.

Это кстати примерная планка того, чего можно добиться сейчас с помощью любого ИИ, если подсказывать ему куда идти. Следующие шаги заставить сделать достаточно сложно, возможно его выборки для обучения не хватило, что из разных статей вычленить информацию о том, какие оптимизации могут оказать конкретное влияние.

1 sec#

Наконец, нормальные решения, чтобы ускориться ещё на один порядок — перестать тыкать структуры данных и посмотреть на алгоритм. Обратить внимание, что ответ попадает в очередь и проверяется лишь на следующем шаге раскрытия вершин. Для поиска в ширину, в котором решение занимает x**N, где N - число шагов раскрытия вершины, уменьшение этапов поиска с 7 шагов до 6 может дать приличное ускорение.

x**7 -> x**6. 18 sec -> 4.1 sec

0.1 sec#

Можно запустить алгоритм с обоих концов, искать не только путь из начальной вершины в конечную, но и из конечной в начальную. Тогда решение найдется не на 7м шаге, где-то между 3м и 4м. Это снижает время с 18 до 0.02 секунд, а вместе с предыдущей оптимизацией ранней проверки — до 0.011 сек

Alexander Stepanov: Three Algorithmic Journeys — хорошая книга про то, что при написании кода важно не забывать о таких простых шагах.

No programmer should have a singlepass mindset.

0.01 sec#

На самом деле до этого этапа, если есть некоторый опыт и интуиции, можно было не пользоваться профайлером.
Теперь можно включить профайлер (лучше увеличить частоту сэмплирования), и посмотреть внимательнее на данные. Если отказаться от общего подхода, и учесть, что в задачке для NES на каждый цвет используется 2 бита цвета, то 16 цветов займут 32 бита, т.е. можно упаковать данные в 32 битное число. Это сокращает время до 0.0075 сек.

0.001 sec#

Можно проводить раскрытие вершины (битовыми операциями), оценку (лучше не выкидывать, что позволит немного ускорить момент обнаружения решения на последнем шаге) и хеширование над этими 32-битами без распаковки.

С хешированием нужно заметить, что есть два способа немного ускорить немного ускорить процесс. Первый — использовать в качестве хеша само запакованное значение. Второй — сделать число слотов в хеш таблице кратным степени двойки числом. Каждый из этих способов по отдельности делает результат лучше, но их нельзя применять одновременно, потому что иначе данные будут стремиться сгруппироваться в определенных слотах. Что-то одно из двух должно “размазать” данные по слотам. Либо хеш-функция должна не зависеть от данных (id - зависит, если данные неслучайны, всякие fnv или murmur - не зависят, std::hash тоже не зависит, но он тормозной). Либо же число слотом должно быть простым/фибоначчи, чтобы при взятии остатка от деления размазывать данные по разным корзинам. С этими оптимизациями получается достичь 0.0007 sec (главное не включать обе, а то будет замедление примерно на 2-3 порядка).

const size_t BUCKETS_COUNT = 2 << 14; //пред-аллокация нужного размера
struct IdHasher {
    MatrixHashT operator() (MatrixHashT value) const { return value; }  //без хеширования
    typedef ska::prime_number_hash_policy hash_policy;                  //политика выбора количества слотов
};
using VertexList = ska::flat_hash_map<MatrixHashT, MatrixHashT, IdHasher>;
static VertexList forwardList(BUCKETS_COUNT); //удаление из замеров вызова конструктора и деструктора

Дальше профайлер подсказывает, что пора заменить priority_queue обратно на vector + 2 указателя на начало и конец очереди, чтобы еще чуть разогнаться.
Получается где-то 0.00075 sec. Еще один порядок скорости достигнут.

С этого места, снова другие хеш-таблицы или структуры, иногда явно худшие:

• google dense hash - 0.0011. Для неё bucket_count всегда степерь двойки, так что с кастомным хешем. Немного медленнее, за счёт того, что ska_flat_map использует robin-good перестановки, чтобы уменьшать худшее время поиска (Robin Hood Hashing should be your default Hash Table implementation). Это даёт буст за счёт того, что данные считываются в кеш пачкой — найти элемент с 1-й попытки или с 5-й по времени одинаково, так как с линейный пробированнием они всё равно окажутся в кеш-линии, замедление будет только если выйти за её пределы. А так - плюс/минус сопоставимый результат.

• 2-threads bidirectional search - 0.065. Можно искать с каждого конца в отдельном треде, синхронизируясь раз в шаг, но переключение тредов всё равно слишком серьёзная операция для таких вещей.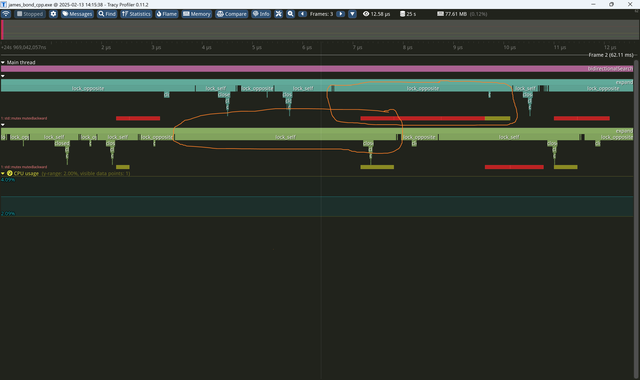
  
  tracy умеет визуализировать время захвата ожидания локов для каждого треда

• bloom-filter. Bloom filter позволяет предварительно проверить наличие элементов в множестве. 0.007 (много дополнительных вызовов функций кеширования?), перед тем как делать еще одно хеширование.

• async search - 0.07. Асинхронные вызовы — это снова скрытая синхронизация, как и с тредами, но спрятанная внутри стандартной библиотеки.

• bytell_hash_map - ещё одна таблица от Malte Skarupke - 0.0011, примерно сопоставима с google dense hash

• bitvector - 0.0011 - просто выделить по биту на каждое возможное значение int, и проверять по индексу тоже почему-то немного медленнее, но на уровне bytell/google_dense_map.

В целом, опуститься ниже 0.00075 сложно. ska::flat_hash_map действительно fastest hash map, с возможностью подтюнить её под свой тип.

Thread-safe hash tables (which are of no use here)#

Явно не подходят для использования в этой задаче, но интересно посмотреть какие они бывают. Кажется пора найти еще одну задачку для исследования и более детального рассмотрения :)

Inside boost::concurrent_flat_map

• взять пачку таблиц и шардировать значения по отдельным, лоча их целиком
• для закрытых хеш-таблиц можно лочить конкретный список значений
• для открытых — хитро высчитывать бакеты, которые нужно залочить. Хитрее, чем кажется %)
• всякие штуки типа “а давайте хранить не значения в бакетах, а бакеты в значениях”. Используется list вместо vector со всеми вытекающими последствиями
• split-ordered-list, кроме указателей на следующие значения хранятся рандомизированные “ускоренные указатели” нескольких уровней, можно лочить башню из указателей по уровням, пока перестраиваются ускоренные, можно продолжать пользоваться более медленными путями поиска.
• here be dragons. Many of them!

Compile-time - 0.0001 sec#

constexpr-версия на fixed_unordered_map. Писать compile-time вычисления на C++ достаточно мутно, компилятор (msvs во всяком случае), просто говорит, что не может сделать функцию compile-time, не уточняя, из-за чего именно. Приходится находить проблемное место бинарным комментированием части кода. Причём то же самое он говорит, если просто не успел вычислить функцию за отведенное время (нужно найти ключи, чтобы дать ему больше времени и памяти). Вдобавок, compile-time вычисления очень медленные (как и Nim, в отличие от F# и daScript). Но тем не менее, в рантайм можно засчитать результат за 0.0000530 (после полуминутных compile-time вычислений).

Приблизительный порядок использования оптимизаций#

• Выбрать подходящие структуры данных
• Выбрать алгоритм и подтюнить его под свой случай
• Оптизировать данные (дискретизировать, запаковать, перекодировать, выровнять, перегруппировать etc). Изучить, как данные лежат в памяти и какие преобразование над ними проводятся. Начать профилировать
• Настроить структуру под свои данные (или написать свою под частный случай, если не настраивается)
• Оптимизировать куски кода с профайлером, посмотреть, во что компируется код и почему
• Посмотреть, можно ли векторизировать или распараллелить части задачи

Любым шагом:

• Посмотреть, что можно посчитать/сгенерировать заранее до выполнения