Spiiin's blog

1 - (2009) Python in imaginary world
2 - (2015) Scala in imaginary world
3 - (2021) Nim in imaginary world
4 - (2022) daScript in imaginary world
5 - (2023) AI in imaginary world
6 - (2024) F# in imaginary world
7 - (2025) C++ in imaginary world

Краткая история моих ковыряний с “задачей Джеймса Бонда-младшего”: когда-то в универе меня восхитил алгоритм поиска в ширину, который подходит для решения практически любой головоломки с состояниями. Я играл на эмуляторе в James Bond Jr., и попробовал решить головоломку с разминированием бомб оттуда этим алгоритмом на языке Python, который тогда как раз начал учить по работе. С тех пор практически традиционно я решаю эту же задачу первой, когда учу новый язык программирования.

Она достаточно сложная, чтобы написать её на новом языке с первого раза, чтобы столкнуться с отладчиком, и достаточно требовательная к вычислениям, чтобы при небрежной реализации столкнуться с необходимостью профилировать её. Также она немного похожа на пятнашки и кубик Рубика, но отличается от них настолько, чтобы алгоритмы для них не подходили, и её плохо распознавал ИИ.

При этом я не особо вдавался в с сам алгоритм, а просто бегло пробовал фичи языков (для версии на C++ — фичи хеш-таблиц).

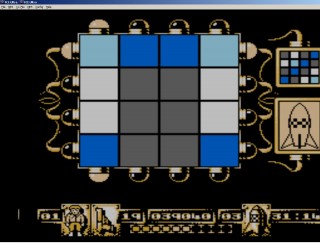
В этот раз чуть-чуть коснусь самой задачи снова на Python (по принципу прототипирования — изучать/пробовать что-то одно, зафиксировав остальное). Условие задачи можно прочитать по первой ссылке в начале поста — необходимо привести поле размером 4x4 из исходного состояния в целевое, сдвигая целиком любую строку или столбец (сдвинутая за границы поля клетка появляется с другой стороны).

BFS#

Если решать задачу честным BFS (жадный поиск в ширину), то потребуется перебрать все позиции на глубину в 8 шагов.
james_bond_python_bfs.py

Если писать это грамотно и без лишних копирований, то на среднем компьютере получится примерно 15-30 сек и 1гб памяти на хранение списка вершин.
Дальше можно запустить поиск с обоих концов (см. пост с версией на C++), и использовать грубую функцию оценки, чтобы на последнем шаге побыстрее выйти на нужную вершину.

Преимущество — простота и гарантированное нахождение минимального пути. Недостаток BFS как алгоритма в его жадности — необходимо много памяти для хранения очереди всех вершин. Поэтому часто хочется находить решения быстрее.

DFS (который не находит минимальный путь)#

Если попробовать использовать DFS (поиск в глубину), то решение тоже найдётся, но путь будет далеко не оптимальным (вместо 8 шагов будет штук 50) — существуют очень длинные решения. Можно придумать различные способы модификации поиска в глубину так, чтобы ограничивать глубину поиска каким-либо образом.

IDDFS#

Простейший метод, если каким-либо образом известна минимальная длина, то просто завершить поиск в глубину по достижении этого пути. При этом нужно не забыть, что с поиском в глубину возможна ситуации, когда позже будет найден более короткий путь между двумя вершинами — необходимо учесть в функции проверки уже посещенных вершин, что при нахождении более короткого пути вершина должна повторно “открыться” для проверки путей к решению через неё.

DFS не требует большого количества памяти, так как вершины раскрываются сразу, но требует эвристики завершения поиска, чтобы не уходить в бесконечно глубокие варианты решений, если путь слишком длинный. Другой недостаток — необходимость повторно исследовать вершины, к которым найден более короткий путь.

IDA*#

Чтобы бороться повторным исследованием вершин в поиска в глубину, функция завершения должна не только опираться на уже пройденный путь и останавливаться по его достижении, но и “смотреть в будущее”, оценивая как скоро можно дойти до решения из текущего состояния. Для того, чтобы находить минимальный путь нужно, чтобы функция оценки давала число ходов до цели не меньше, чем действительное число ходов. Это требование уже зависит от конкретной задачи и требует аккуратных расчётов.

Я своих первых поисках не учёл это требование, из-за чего пропускал самое короткое решение в 8 шагов, и находил только решения за 9 шагов.

Как правильно построить функцию оценки?

Можно оттолкнуться от того, что за 1 ход двигается 4 клетки. Следовательно в лучшем случае 4 клетки сдвинутся в направлении своих позиций на 1 шаг. Необходимо опираться только на эту лучшую оценку (без дополнительных сведений о поле). Оценку шагов до своих позиций посчитать несложно (сложно посчитать её быстро 😂) — у всего этого есть умные названия “тороидальное манхеттенское расстояние” и “венгерский алгоритм назначения”. Но есть и сильно упрощающая вычисления идея — шаги по вертикали и горизонтали можно считать отдельно (так как нет ходов, которые делали бы одновременно вертикальный и горизонтальный сдвиг), и брать их сумму.

Korf — тут описаны эвристики для кубика Рубика, почти аналогичные.

Главное правило — нельзя забывать, что полученные числа необходимо делить на 4, как если бы в идеальном случае каждый сдвиг всегда двигал все 4 элемента в нужных направлениях (оценка должна всегда быть не хуже, чем идеальный путь к цели, чтобы наш путь оставался самым коротким).

james_bond_python_ida.py

Тада! Теперь решение действительно самое короткое, и находится всего за 8.5 секунд и потребляет 15 мб памяти (против 17 секунд и 1500мб у BFS).

Убираем повторные ходы#

Кроме того, чтобы поправить функцию оценки, можно также коснуться и функции раскрытия вершины, то есть генерации доступных ходов. В простейшем случае к позиции просто применяются 16 доступных ходов — сдвиги каждой строки влево-вправо и вверх и вниз. Дальше получившаяся позиция проверяется через хеш-таблицу. Такая проверка для больших значений недешёвая, так что можно воспользоваться знанием о предыдущих шагах для того, чтобы избегать повторной генерации поля.

Бывают ходы:

• ничего не меняющие: если все клетки строки/столбца одного цвета , нет смысла выполнять такой ход
• обратные: после сдвига влево нет смысла сдвигать эту же строку вправо (аналогично для столбцов)
• коммутативные: сдвиг сначала первой строки, а затем второй эквивалентен сдвигу второй строки, а затем первой

Еще пара более комбинированных правил:

• три сдвига в одну сторону эквивалентны одному сдвигу в обратную
• блок сдвигов по строкам (или столбцам) можно рассматривать целиком. В пределах этого блока должны соблюдаться все правила выше, т.е. если какая-либо строка уже была сдвинута в определенную сторону, она до сдвига столбца не должна быть сдвинута в ту же сторону.
• В пределах блока сдвигов также должна соблюдаться коммуникативность ходов — можно рассматривать только непонижающиеся номера строк

Таким образом отсеивается из генерации где-то восьмая часть ходов.
james_bond_python_ida_dedup.py

Это даёт примерно соразмерный убранным проверкам прирост производительности — с 8.5 до 7 секунд.

Что можно было бы улучшить ещё#

В алгоритме Корфа также описана идея рассчитать заранее оценки для некоторых позиций, но c compile-time вычислениями я уже наигрался.

В решателе кубика Рубика Kociemba встречается идея вставлять в планирование между исходным состоянием и целевым промежуточные известные “хорошие” состояния вместо слепой генерации, чтобы избежать топтания генератора вокруг локальных минимумов. В головоломках с запутанными между собой группами небольшое количество элементов не на своих местах необязательно означают близость решения, но определенные состояния могут намекать на частично собранный пазл. Но для обнаружения таких состояний нужно лучше изучить структуру головоломки. Хотя некоторые коммутаторы для кубика Рубика подходят (например, последовательность LeftX, UpY, RightX, DownY циклически переставляет три элемента местами, не меняя положение остальных).