Spiiin's blog

О вычислительной геометрии#

С вычислительной геометрией есть такая штука, что, кажется, её мало где изучают. С какой-то вероятностью средний игровой программист будет знать что-то о компьютерной графике и немного общей математики, но шанс того, что он знает алгоритмы вычислительной геометрии из университета, невелик.

При этом для понимания алгоритмов, например, определения коллизий или игровой физики, необходима хорошая геометрическая интуиция, то есть понимание того, как изменения в формулах влияют на поведение объектов в плоскости/пространстве. Это нужно как для общего представления о работе алгоритмов, так и для улучшений — можно получить ускорение за счёт правильного порядка применения операций, устранения избыточных вычислений, или понимания особенностей данных (например, если объекты для проверки — юниты, которые в основном ходят по земле, то разброс координат по высоте у них будет небольшой).

Эту интуицию сложно наработать без хорошей среды-песочницы в которой можно было бы поиграться с формулами и подвигать объекты. Но создание такой среды, может занять много времени. Например, относительно просто набросать opengl приложение, но создать вокруг него обвязку, чтобы можно было отображать и двигать точки, прямые, плоскости, сферы, углы и так далее — по времени может быть дольше, чем реализовывать сам алгоритм.

Геометрические алгоритмы, что неудивительно, часто имеют какую-нибудь геометрическую интерпретацию, которую можно визуализировать и “пощупать” для отладки, или создания альтернативной референсной версии для сравнения (что тоже инструмент отладки), так что могут быть полезны и не только в образовательных целях.
Robustification Through Introspection and Analysis Tools (Avoiding Developer Taxes) — доклад от Valve о том, что проще “выдрать” нужные данные из движка/игры и перекинуть в альтернативное приложение для удобной отладки физики.

При этом сложно найти простую и бесплатную программу для визуализации 3d геометрии, в которой был бы готовый функционал для построений.

В чем построить 3d сцену для визуализации алгоритма#

Python с его NumPy/SymPy/Matplotlib или аналоги. Не очень хорош в том, чтобы работать с зависимыми обновляемыми объектами. NumPy требует отдельного курса изучения для нормальной работы, отдельной среды для удобной интерактивной работы с 3d геометрией нет. Всякие Julia и подобные среды хуже.
Blender, Unity или другие среды работы с 3d объектами/движки. В принципе удобнее, и есть примитивы для работы с 3d-объектами. Удобство построений зависит от опыта работы в этих средах.
Mathematica, Matlab и подобные среды - удобно, но платно.
Свой движок - удобно, но трудоёмко. Для движков часто выбор языка - С++ + голое графическое API, не самый удобный для создания отладочного функционала (описания зависимых объектов и гуи для интерактивных манипуляций).
Среды интерактивной геометрии (Geogebra, Desmos) - просто, бесплатно и удобно, но часто слишком примитивно, и 3d функционал намного более ограниченный, чем 2d. Работают с ограниченным языком, на котором сложно писать свои функции.
Prototyping frameworks (rendering) — список фреймворков для визуализации, для рендер-программистов (цели в чем-то похожи, но дополнительно включают доступ к графическому API и настройке шейдеров/материалов).

У каждого подхода свои плюсы и минусы, мне показались наиболее интересными среды для интерактивной геометрии, например, Geogebra. В ней есть пачка готовых команд для построения примитивов. Мне нравятся максимально интерактивные подходы для обучающих сред:
Inventing on Principle by Bret Victor
Learnable Programming
Интерактивная геометрия на примере кривых Безье

В Geogebra хватает интерактивности, но скудные возможности по программированию. Есть javascript api, которое позволяет сгенерировать строковую команду для среды и выполнить её, но это API скорее годится как конструктор для построения среды, а не как интерактивный редактор. Также есть прототип среды на Python поверх этого API (на Skulpt), реализованный и кажется брошенный авторами (доклад). В прототипе реализована работа с 2d-объектами, но после некоторого ковыряния, мне удалось завести его для 3d. После базовой настройки я скормил её cursor-у. Фактически — добавление новых команд, это создание тривиальных новых обёрток. Причём среда поддерживает live-reload, так получается вообще интерактивно и лениво добавлять команды без перезапуска, одно из хороших применений ИИ (без вникания в typescript и api биндингов skulpt).

https://github.com/spiiin/pyggb_3d

Выглядит так:

Ссылки на другие объяснения GJK#

Вот список хороших объяснений:
Real-time collision detection book — объяснение с теорией и возможными оптимизациями, глава из книги Christer Ericson.
Implementing GJK — подробное объяснение от Casey Muratori.
Two Different & Unknown GJK Algorithms, Visualized, Implemented, and Explained — объяснение двух версий GJK, с визуализацией на Jai

GJK: Collision detection algorithm in 2D/3D — ещё одно, с визуализацией в 2d, но объяснениями 3d (кажется, с ошибкой, но без визуализации в 3d сложно перепроверить).

Объяснение в книге у Christer Ericson просто с иллюстрациями, у Casey — на слайдах и “на пальцах”, а код на Jai не запустишь, чтобы поиграться, так как компилятора нет в открытом доступе. Собственно, вот момент в объяснении Casey, где он пытается показать, что направление в 3d может быть совсем не такое, как выглядит на 2d рисунке, и объясняет, что если забыть про это, то можно сломать алгоритм, или что хуже, просто ухудшить сходимость. После этого я подумал, что нужно попробовать сделать визуализацию, чтобы про алгоритм не рассказывать, а показывать построения, которые можно подвигать самому.

GJK#

Алгоритм определения коллизий GJK включает пачку вспомогательных трюков из вычислительной геометрии, которые можно попробовать визуализировать в ходе объяснения. Сами эти трюки достаточно простые.

Для начала — есть 2 алгоритма GJK. Один только определяет наличие пересечения (и оптимизирован для этого), второй отслеживает ближайшие друг к другу части объектов (например, чтобы можно было с помощью EPA определить глубину проникновения и вектор расталкивания объектов). Тут будет реализация первого алгоритма, "boolean-GJK".

Сумма Минковского#

Сразу же — вспомогательные трюки. Сумма Минковского для двух векторов A и B — это множество, состоящее из сумм всех векторов из A и B. Для определения пересечений используют “разность Минковского” (это не обратная сумме операция, а сумма с отраженными векторами B, поэтому иногда называется отдельно — translation configuration space obstacle, TCSO).

Если объекты пересекаются, то их разность включает точку начала координат.

Работать с этой разностью в общем случае сложно (произведения каждой точки внутри объёма фигуры), поэтому, как и для большинства алгоритмов в вычислительной геометрии, рассматриваются только выпуклые фигуры. Они обладают полезным свойством, что если точка расположена дальше всех своих соседей относительно какого-либо направления, то она является самой дальней в этом направлении для всей фигуры. Таким образом, можно исследовать не все точки внутри фигуры, а только её вершины (ну или, например, выразить аналитически крайние точки сферы или циллиндра).

Интуиция для разности Минковского достаточно простая. Вместо того, чтобы проверять пересечение игрока и препятствия сложной формы мы расширяем препятствие на размер игрока и проверяем пересечение простой точки с этой нарощенной фигурой. Это может быть выгодно тем, что пересечение можно закешировать и, если объекты не изменились, не вычислять его повторно. А также тем, что разность находится ближе к началу координат, чем позиция в мировых координатах, а значит вычисления производятся с большей точность в мантиссе

Разность Минковского для двух пирамидок на geogebra-python:

def prism(pt):
    vals = [(pt[0] + p[0], pt[1] + p[1], pt[2] + p[2]) for p in [(3, 3, 0), (5, 3.24, 0), (4, 4.75, 0), (4, 3.7, 2)]]
    
    A, B, C, D = Point(*vals[0]), Point(*vals[1]), Point(*vals[2]), Point(*vals[3])
    seg1 = [Segment(B, C), Segment(C, A), Segment(A, B)]
    seg2 = [Segment(B, D), Segment(D, A), Segment(A, B)]
    seg3 = [Segment(C, D), Segment(D, B), Segment(B, C)]
    seg4 = [Segment(A, D), Segment(D, C), Segment(C, A)]
    faces = Polygon([A, B, C]), Polygon([A, B, D]), Polygon([B, C, D]), Polygon([C, A, D])
    return A, B, C, D
    
pts1 = prism((3,0,0))
pts2 = prism((0,0,0))

diffPoints = []
diffPointsProj2d = []
for p1 in pts1:
    for p2 in pts2:
        diffPt = p2 - p1
        diffPoints.append(diffPt)
        diffPtProj = TranslateI(diffPt, VectorI(PointI(0 ,0, -diffPt.z)))
        diffPointsProj2d.append(diffPtProj)
hull2d = ConvexHull(diffPointsProj2d)

(я добавил версии команд Geogebra с I на конце, для более краткого создания невидимых вспомогательных фигур)

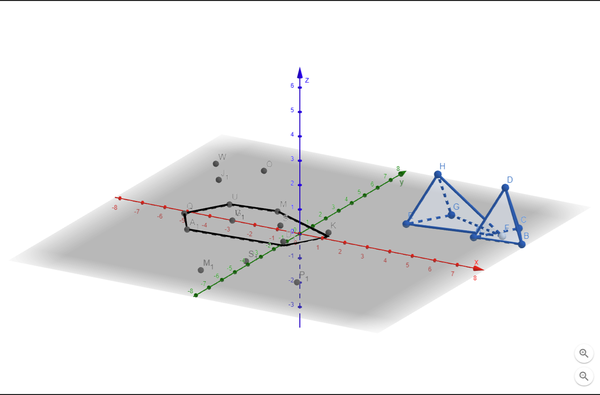
https://www.geogebra.org/3d/fjpbz4cb

Если подвигать любую точку, изменится и разность Минковского. Визуализируются только крайние точки, разностью является выпуклая оболочка (convex hull) вокруг всех этих точек и все точки внутри оболочки, но строить 3d convex hull вокруг точек это отдельный непростой алгоритм, поэтому я просто спроецировал точки на плоскость xy и построил 2d convex hull, просто чтобы было лучше видно точку начала координат (то что она находится внутри этой проекции необязательно означает, что она находится внутри реального Convex Hull-а, в этом и прелесть визуализации, что можно подвигать точки и обнаружить это!).

Да и строить честный convex hull в 3d не нужно, потому что алгоритм GJK использует еще один трюк, и обращается вычисляет только экстремальные точки разности Минковского (самые дальние в каком-нибудь направлении).

Support points#

Support point (иногда support mapping, пусть будет “опорная точка”) — самая дальняя точка фигуры в заданном направлении.

points = prism()
O = Point(0, 0, 0)

dirPoint = Point(0, 1, 0, caption = "Dir")
dirVector = Vector(O, dirPoint)

support_planes = [PerpendicularPlaneI(support_point, dirVector) for support_point in points]

@dirPoint.when_moved
def on_moved():
    proj = [Dot(dirVector, VectorI(O, p)) for p in points]
    max_proj = max(proj)
    max_index = proj.index(max_proj)
    for i, support_plane in enumerate(support_planes):
        support_plane.is_visible = i == max_index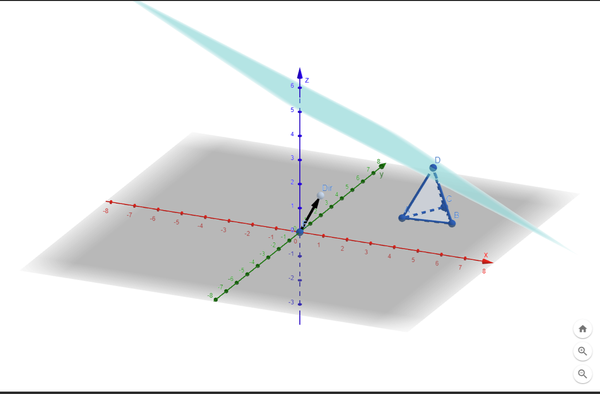

https://www.geogebra.org/3d/d5ax94yr

Вычисляется просто как максимальная проекция из всех точек на вектор направления. В визуализации можно повертеть вектор и посмотреть, как меняется опорная плоскость (и убедиться, что эта никакие точки фигуры не выходят дальше за эту плоскость).

Support point для разности Минковского это разность support point фигуры A в том же направлении, и фигуры B в противоположном направлении:

Support(A-B) = SupportA(d) - SupportB(-d)

Т.е. вместо обращения к разности Минковского за точкой, можно вычислить support point исходных фигур. Это трюк позволяет отказаться от расчёта разности Минковского — вместо перебора всех её точек, нужно перебрать все точки каждой из фигур по отдельности.

Кроме того, чтобы перебирать все точки каждой из фигур, могут использоваться приёмы для ускорения поиска, основанные на знании о геометрии исходных фигур:

• если известны соседи вершин, то перебираются соседи до тех пор, пока проекция увеличивается (hill climbing). Это работает только для выпуклых фигур
• если “ползти” только по соседям слишком долго (в худшем случае на противоположную сторону фигуры), то добавляются проверки не только соседей, но и более удаленных точек, чтобы можно было более быстро “перепрыгнуть” на экстремальную точку. В реальных приложениях все эти расчёты могут делаться на стадии подготовки геометрии. Таким же образом решается проблема фигур, у которых грани лежат в одной плоскости (кубик с гранями из двух треугольников)
• можно считать экстремальную точку простых фигур аналитически (например, для сфер)

Симплексы#

Следующий трюк алгоритма основан на Carathéodory’s theorem. Для любой точки внутри выпуклой фигуры (а разность Минковского для двух выпуклых фигур является выпуклой фигурой) в трехмерном пространстве существует такой симплекс из вершин этой фигуры, который бы содержал эту точку. Симплекс для 3d - это пирамида.

Алгоритм GJK заключается в том, чтобы попытаться построить симплекс из вершин разности Минковского, содержащий точку O (начало координат), на каждом шаге перестраивая частично построенный симплекс так, чтобы его точки были всё ближе к началу координат. Если такой симплекс построен, то фигуры пересекаются, если же алгоритм доходит до ближайшего к O симплекса, не содержащего O - то пересечения нет.

Может быть написано заумно, но на самом деле тривиально:

pts1 = figure1()
pts2 = figure2()

def find_furthest_point(obj, direction):
    proj = [Dot(direction, VectorI(O, p)) for p in obj]
    max_proj = max(proj)
    max_index = proj.index(max_proj)
    return obj[max_index]

def get_support(obj1, obj2, direction):
    a = find_furthest_point(obj1, direction)
    b = find_furthest_point(obj2, Invisible(-direction))
    return Invisible(a - b)

def gjk(pts1, pts2):
    current_points = [] # simplex
    support = get_support(pts1, pts2, VectorI(O, PointI(0, 0, 1))) # any direction as first step
    current_points.append(support)
    direction = VectorI(support, O)
    while True:
        support = get_support(pts1, pts2, direction)
        current_points = [support, *current_points] # new point for simplex added as first point!
        if Dot(VectorI(O, support), direction) <= 0:
            return False #no collision
        is_finish, direction = next_step(current_points, direction)
        if is_finish:
            return True

• начальное направление выбирается произвольно (на практике для оптимизации может быть закешированное направление, полученное с прошлого запуска работы алгоритма). В этом направлении находится первая опорная точка. Затем алгоритм пытается найти следующую точку в направлении от первой точки к началу координат.
• next_step - это функция, которая берёт частично построенный симплекс и текущее направление, в котором нужно его достраивать, и смотрит, что нужно сделать следующим шагом. При этом возможны различные ситуации, которые будут разобраны дальше. Функция может продолжать строить симплекс, добавляя в него новую точку, или отбросить одну или несколько старых точек, вернувшись на шаг назад. При этом алгоритм гарантирует, что после отбрасывания и добавления новой точки итоговый симплекс будет ближе к точке O, чем до отбрасывания, то есть алгоритм не зациклится (хе-хе, если реализован без ошибок). Также функция выбирает новое направление, в котором нужно искать следующую опорную точку. Направление не указывает на саму точку, а рассчитывается в зависимости от того, к какой части симплекса (региону Вороного) находится ближе точка O.

Дальше нужно рассмотреть все возможные случаи, которые могут возникнуть в next_step.
Для точки следующий шаг тривиален — выбирается вторая точка в направлении к O.

Line case#

Посмотрим, что получается, когда построена линия

debugPlanes = True
debugDir = True

A = Point(2, 1.1, 0)
B = Point(-1.25, -6.3, 3.2)
O = Point(0, 0, 0, caption = "O")

ab = Vector(A, B)
ao = Vector(A, O)
n = CrossI(ab, ao)
newDir = CrossI(n, ab)

p1 = PerpendicularPlane(A, n, is_visible = debugPlanes)
p2 = PerpendicularPlane(A, newDir, is_visible = debugPlanes)

if debugDir:
    C = MidpointI(A,B)
    debugNewDir = Vector(C, Invisible(C + UnitVectorI(newDir)), color = "blue")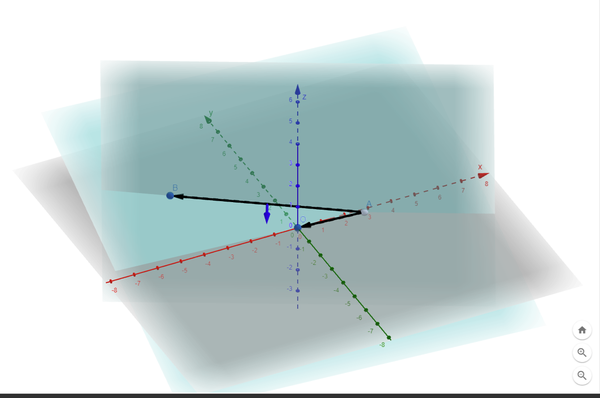

https://www.geogebra.org/3d/kagfzmtz

Это как раз та часть алгоритма, которая в 3d отличается от 2d, и визуализация помогает лучше представить, как именно выбирается следующее направление.

Тут сначала стоит обратить внимание на то, что в разборе GJK стандартно точка A представляет новую добавленную в симплекс точку. Мы знаем, что мы “пришли” в точку A из точки B, когда выбирали support point в направлении O. Следующее направление должно быть выбрано как перпендикуляр к этой прямой, направленный в сторону к точке O.

Это построение не очень понятно описывается словами и плохо видно на 2d рисунках, так как проецирует наклон “к зрителю” в одну и ту же прямую, перпендикулярную AB. Но его легко понять в 3d построении, подвигав точки A и B.

Строится вектор, перпендикулярный ABO, и от него, еще один, лежащий в плоскости ABO и перпендикулярный AB (этот вектор позволит найти support point для AB — самую дальнюю от вектора точку в направлении O).

Triangle case#

После того, как добавилась третья точка, нужно оценить отношение построенного треугольника к точке O. Это самая запутанная часть, но попробуем визуализировать и её:

A = Point(-1, -1, 0)
B = Point(-1.2, 1.5, 0)
C = Point(1.2, -0.6, 0)

bca = CrossI(VectorI(B,C), VectorI(B,A))
p = Plane(B, VectorI(B,C), bca, is_visible = True)

P = Point(-3, -3, 3)
p_normal = CrossI(bca, VectorI(B,C))
d = Dot(p_normal, VectorI(B, P))

Pclip = If(
    Function.compare_LT(d, Number(0)),
    ClosestPointI(p, P),
    P
)

segments = [Segment(A,B), Segment(A,C), Segment(B,C)]
tri = Polygon([A,B,C])

#debug
debugLines = True
lineAB = Line(A,B, is_visible = debugLines)
lineAC = Line(A,C, is_visible = debugLines)

ab = VectorI(A, B)
ac = VectorI(A, C)
bc = VectorI(B, C)
ap = VectorI(A, Pclip) #vector to point
bp = VectorI(B, Pclip) #vector to point

abc = CrossI(ab, ac)
directionFromAC = CrossI(CrossI(ac, ap), ac)
directionFromAB = CrossI(CrossI(ab, ap), ab)

#for side resolution
sameDir_abcac_ap = Dot(CrossI(abc, ac), ap)
sameDir_ac_ap = Dot(ac, ap)
sameDir_ababc_ap = Dot(CrossI(ab, abc), ap)
sameDir_ab_ap = Dot(ab, ap)

#debug render direction from AC
midAC = MidpointI(A, C)
dirAC = Vector(midAC, Invisible(midAC + UnitVectorI(directionFromAC)))

#debug render direction from AB
midAB = MidpointI(A, B)
dirAB = Vector(midAB, Invisible(midAB + UnitVectorI(directionFromAB)))

#debug render direction from A
dirBC = Vector(A, Invisible(A + UnitVectorI(ap)))

#debug render direction from ABC face
center = CentroidI(tri)
centerDir = If(
    Function.compare_LT(Dot(abc, ap), Number(0)),
    PointI(0, 0, 1),
    PointI(0, 0, -1)
)
centerDir.is_visible = False
dirABC = Vector(center, Invisible(center + centerDir))

@A.when_moved
@B.when_moved
@C.when_moved
@P.when_moved
def on_moved():
    on_ac_side = sameDir_abcac_ap > 0 and sameDir_ac_ap > 0
    on_ab_side = sameDir_ababc_ap > 0 and sameDir_ab_ap > 0
    on_a_side = sameDir_abcac_ap > 0 and sameDir_ababc_ap > 0
    on_tri_side = not (on_ac_side or on_ab_side or on_a_side)
    dirAC.color = "green" if on_ac_side else "black"
    dirAB.color = "green" if on_ab_side else "black"
    dirBC.color = "green" if on_a_side else "black"
    dirABC.color = "green" if on_tri_side else "black"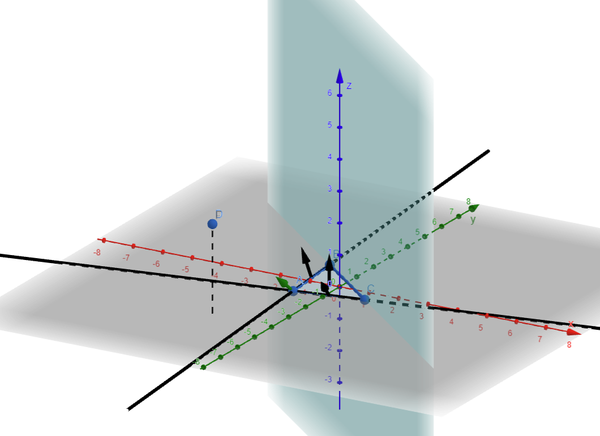

https://www.geogebra.org/3d/gfmp3qne

Я здесь вместо O использовал точку P, чтобы показать отношение точки, которую можно двигать и треугольника. В общем случае точка P может находится в 7 положениях относительно треугольника — ближе к каждой из трех вершин, ближе к каждой из трёх сторон, или “ближе к самой грани” (выше или ниже, это считается за один тип).

Но если использовать знание, что мы на прошлом шаге “пришли” из отрезка BC, добавив к нему точку A в направлении O (или P как в визуализации), то окажется, что точка P не может находиться в областях за BC. Тогда остаются только 4 региона:

• ближе к ребру AB
• ближе к ребру AC
• ближе к вершине A
• ближе к грани ABC, выше или ниже ABC

Визуализация ограничивает движение точки P так, чтобы она не выходила за ребро BC, и показывает для каждого из 4х случаев возможный вектор, также строит линии, которые отображают границы регионов, и подсвечивает активный вектор, который будет выбран, зелёным. Одновременные повороты всех векторов нагляднее, чем построение вектора для отдельной линии.

Действия в каждом из случаев понятны — оставляем ту часть, которая ближе и искомой точке, и отбрасываем дальнюю точку или ребро. Если же “захватили” точку под или над треугольником, то пытаемся найти оставшуюся четвертую точку, так чтобы пирамида содержала эту точку. Единственная особенность — нужно не забыть про правильный порядок точек, чтобы сохранить направления нормалей.

Pyramid case#

Тут тривиальный случай — просто проверяется с какой стороны от треугольника лежит точка. Если с внешней относительно призмы — отбрасываем дальнюю точку и снова возвращаемся к случаю с треугольников. Если же для каждого из треугольников точка лежит внутри — ура, мы достроили симплекс, и нашли пересечение.

Полный код#

initial_objects = []
final_objects = []

# remove auxilary objects
def clear_objects(initial_objects, final_objects):
    for obj in final_objects:
        if obj not in initial_objects:
            deleteObject(obj)

def prism(pt):
    vals = [(pt[0] + p[0], pt[1] + p[1], pt[2] + p[2]) for p in [(3, 3, 0), (5, 3.24, 0), (4, 4.75, 0), (4, 3.7, 2)]]
    
    A, B, C, D = Point(*vals[0]), Point(*vals[1]), Point(*vals[2]), Point(*vals[3])
    seg1 = [Segment(B, C), Segment(C, A), Segment(A, B)]
    seg2 = [Segment(B, D), Segment(D, A), Segment(A, B)]
    seg3 = [Segment(C, D), Segment(D, B), Segment(B, C)]
    seg4 = [Segment(A, D), Segment(D, C), Segment(C, A)]
    faces = Polygon([A, B, C]), Polygon([A, B, D]), Polygon([B, C, D]), Polygon([C, A, D])
    return A, B, C, D
    
pts1 = prism((3,0,0))
pts2 = prism((2,0,0))
O = Point(0, 0, 0, caption = "O")

diffPoints = []
for p1 in pts1:
    for p2 in pts2:
        diffPt = p1 - p2
        diffPt.caption = ""
        diffPoints.append(diffPt)
        
def find_furthest_point(obj, direction):
    proj = [Dot(direction, VectorI(O, p)) for p in obj]
    max_proj = max(proj)
    max_index = proj.index(max_proj)
    return obj[max_index]

def get_support(obj1, obj2, direction):
    a = find_furthest_point(obj1, direction)
    #a.color = "red"
    b = find_furthest_point(obj2, Invisible(-direction))
    #b.color = "red"
    return Invisible(a - b)
    
def next_step(simplex, direction):
    def line(simplex, direction):
        a, b = simplex[0], simplex[1]
        ab = VectorI(a, b)
        ao = VectorI(a, O)
        if Dot(ab, ao) > 0:
            return False, CrossI(CrossI(ab, ao), ab)
        else:
            simplex[:] = [a]
            return False, ao
        return False, None
        
    def triangle(simplex, direction):
        a, b, c = simplex[0], simplex[1], simplex[2]
        ac = VectorI(a, c)
        ao = VectorI(a, O)
        ab = VectorI(a, b)
        abc = CrossI(ab, ac)
        if Dot(CrossI(abc, ac), ao) > 0:
            if Dot(ac, ao) > 0:
                simplex[:] = [a, c]
                return False, CrossI(CrossI(ac, ao), ac)
            else:
                simplex[:] = [a, b]
                return line(simplex, direction)
        else:
            if Dot(CrossI(ab, abc), ao) > 0:
                if Dot(ab, ao) > 0:
                    simplex[:] = [a, b]
                    return False, CrossI(CrossI(ab, ao), ab)
                else:
                    simplex[:] = [a]
                    return ao
            else:
                if Dot(abc, ao) > 0:
                    return False, abc
                else:
                    simplex[:] = [a, c, b]
                    return False, Invisible(-abc)
        return False, None
        
    def prism(simplex, direction):
        a,b,c,d = simplex[0], simplex[1], simplex[2], simplex[3]
        abc = CrossI(VectorI(a, b), VectorI(a, c))
        acd = CrossI(VectorI(a, c), VectorI(a, d))
        adb = CrossI(VectorI(a, d), VectorI(a, b))
        ao = VectorI(a, O)
        if Dot(abc, ao) > 0:
            simplex[:] = [a, b, c]
            return triangle(simplex, direction)
        if Dot(acd, ao) > 0:
            simplex[:] = [a, c, d]
            return triangle(simplex, direction)
        if Dot(adb, ao) > 0:
            simplex[:] = [a, d, b]
            return triangle(simplex, direction)
        return True, None
    
    #print(simplex)
    if len(simplex) == 2:
        return line(simplex, direction)
    if len(simplex) == 3:
        return triangle(simplex, direction)
    if len(simplex) == 4:
        return prism(simplex, direction)
    return False, direction

def draw_debug_simplex(current_points):
    for current_point in current_points:
        current_point.is_visible = True
        current_point.color = "blue"
    for i in range(len(current_points)):
        for j in range(i + 1, len(current_points)):
            seg = Segment(current_points[i], current_points[j])

def gjk(pts1, pts2):
    current_points = []    
    support = get_support(pts1, pts2, VectorI(O, PointI(0, 0, 1))) #any direction as first step
    current_points.append(support)
    direction = VectorI(support, O)
    max_steps = 50
    while True:
        max_steps -= 1
        if max_steps == 0:
            print("50 steps", len(current_points)) # should never happen
            #draw_debug_simplex(current_points)
            return False
        support = get_support(pts1, pts2, direction)
        current_points = [support, *current_points]
        if Dot(VectorI(O, support), direction) <= 0:
            draw_debug_simplex(current_points)
            return False #no collision
        is_finish, direction = next_step(current_points, direction)
        if is_finish:
            draw_debug_simplex(current_points)
            return True

def when_point_clicked():
    global initial_objects, final_objects
    clear_objects(initial_objects, final_objects)
    intersect = gjk(pts1, pts2)
    O.color = "green" if intersect else "red"
    print(intersect)
    #print(len(initial_objects), len(final_objects))
    final_objects = getAllObjectNames()

for p in pts1: p.when_moved(when_point_clicked)
for p in pts2: p.when_moved(when_point_clicked)


initial_objects = getAllObjectNames() # remembers object before doing gjk
when_point_clicked()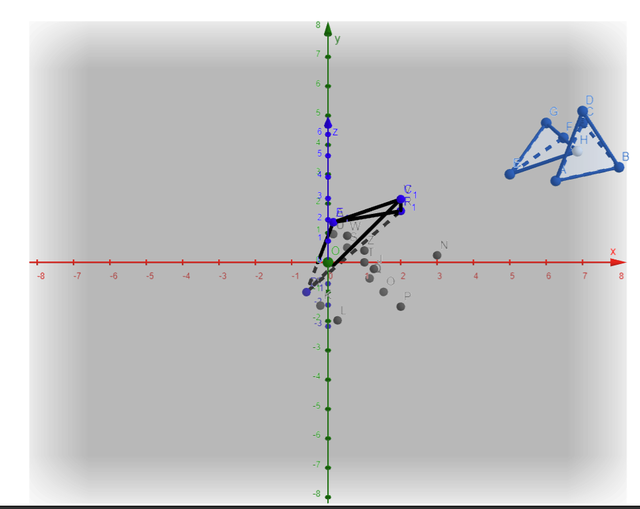

линк
(любое передвижение точек призм вызывает перестройку симплекса, определяющего пересечение)

Тут обычно серия рассуждений о применимости GJK в разных случаях, но этого и в других туториалах хватает.

update - исправил пачку ошибок и допилил удаление возможность удаления временных объектов, теперь можно перестраивать симплекс на движение любой точки. оооооу, моя геогебра!

Код примеров:
https://github.com/spiiin/pygbb_3d_examples

Вывод#

Среда немного сыровата, но в принципе позволяет пользоваться всеми возможностями Geogebra для построений, при этом вполне встраивается в код на Python (но всё равно стоит помнить о том, что в скриптах скрещены два отдельных мира). Так что задумку можно было бы и допилить, если мне приспичит разобраться с ещё какими-нибудь алгоритмами.