- Geogebra, Python и GJK — первая заметка о визуализации алгоритмов вычислительной геометрии в
Geogebra.
Докрутил немного среду для удобства визуализации, выложил веб-версию, и собрал ещё один туториал про упомянутый в первой статье метод построения выпуклой оболочки (ConvexHull) в 3D.
Для разбора взят метод Джарвиса (заворачивание подарка). Он не самый быстрый, но наглядный, так что также подходит для тренировки геометрической интуиции перед реальной реализацией.
Более серьёзное и хорошее описание алгоритма есть в книге Препарата и Шеймос - Вычислительная геометрия: введение (Раздел 3.4 Выпуклые оболочки в пространствах размерности большей двух). Метод обобщается на любые размерности, для простоты рассматривается симплициальные политопы (для 3д - состоящие невырожденных треугольников не лежащих в одной плоскости), но можно улучшить и для более общих случаев.
Идея алгоритма заключается в последовательном переходе от одной известной гиперграни (грани с нормалью) оболочки к смежной, примерно как происходит заворачивание в лист бумаги. Для симплициальных политопов одно ребро выпуклой оболочки является общим для в точности для двух граней. Таким образом, если хранить текущий список ребёр (текущий “периметр” оболочки), то на каждом шаге можно раскрывать одно из таких ребёр — смотреть, какая новая грань прилегает к этому ребру и добавлять новые два ребра (если для них еще не были найдены обе прилегающие к ним грани) к списку ребёр “периметра” оболочки.
Первая подзадача — найти какую-нибудь начальную грань выпуклой оболочки. Это частный случай общей задачи нахождения грани по известному ребру.
Для начала выберем какую-нибудь первую точку этой грани.
# Создаем несколько случайных точек
pts = []
def rand_point(maxValue):
return Point(maxValue*random(), maxValue*random(), maxValue*random())
for i in range(8):
r = rand_point(5)
r.caption = str(i)
pts.append(r)
def find_initial_point(pts):
return min(pts, key=lambda p: p.z)
p0 = find_initial_point(pts)
p0.color = "green"Первой точкой можно выбрать самую экстремальную в каком-нибудь направлении, например, нижнюю (если их несколько, то еще и самую левую из нижних, если будет строить оболочку заворачиванием вправо).
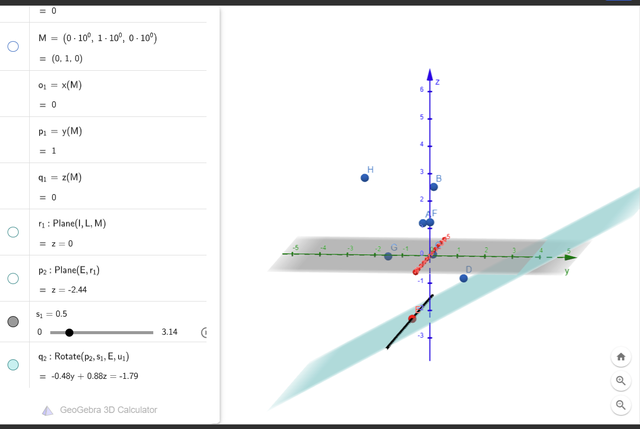
Следующим шагом сделаем визуализацию идеи, как происходит “заворачивание” плоскости вокруг точки, чтобы понять, как найти вторую точку начальной гиперграни. Будем вращать плоскость вокруг какой-нибудь оси. При этом нам также нужно следить за нормалью гиперграни — мы хотим оборачивать плоскость с внешней стороны полигона, а нормаль как раз подсказывает, какая из сторон внешняя.
O = PointI(0, 0, 0)
px = PointI(1, 0 ,0)
pz = PointI(0, 0, 1)
xDir = VectorI(O, px)
l = Line(p0, Invisible(p0 + xDir)) # Строим линию от начальной точки в направлении xDir
planeXYO = Plane(O, PointI(1, 0, 0), PointI(0, 1, 0), is_visible = False) # плоскость XYO
plane0 = Plane(p0, planeXYO, is_visible = False) # строим параллельную XYO плоскость, проходящую через начальную точку гиперграни
# интерактивная визуализация, создаём слайдер для того, чтобы менять угол наклона плоскости
angleToRotate = Slider(0, 3.14)
plane0_rot = Rotate(plane0, angleToRotate, p0, xDir) # поворачиваем плоскость на угол, заданный слайдером
plane0_rot.color = "green"Тут можно повращать плость и заметить, что правый край “поднимается”, и первой встреченной плоскостью точкой будет D.
Чтобы найти эту точку алгоритмически, необходимо найти минимальный угол между плоскостью XYO и плоскостями, которые содержат каждую из точек при вращении.
Это самая сложная часть алгоритма, и я не буду визуализировать её тут (потому что тянет на отдельный туториал по проекциям). Вот рисунок проекций из книги Препарата, просто как иллюстрация, что не помешала бы нормальная визуализация: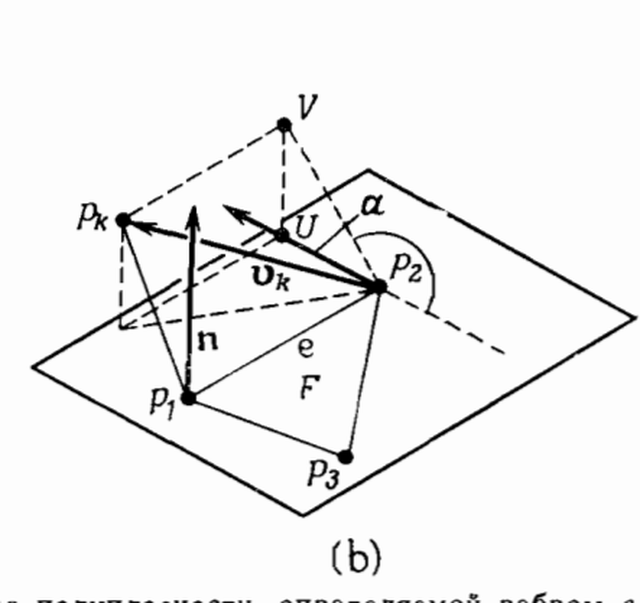
def angle_about_axis(v, axis, reference_normal):
# Угол между нормалью и вектором, проецированным на вращающуюся плоскость
# Перпендикулярная компонента вектора v относительно оси вращения:
v_perp = CrossI(axis, CrossI(v, axis)) # = v - proj_v_on_axis
angle = math.atan2(
Dot(CrossI(reference_normal, v_perp), axis).value, # Синусовая часть
Dot(reference_normal, v_perp).value # Косинусовая часть
)
return angleУгол между двумя векторами — объяснение от _winnie, почему искать углы лучше через atan2, чем через arccos (а лучше вообще не искать углы, но это уже часть об оптимизациях, а не об общем алгоритме).
Третья точка ищется таким же способом — первые две точки образуют линию, относительно которой мы теперь будем вращать плоскость. Третья точка передаются в функцию, чтобы можно было восстановить нормаль к плоскости, так что порядок передачи точек важен (он определяет направление вращения к следующей точке)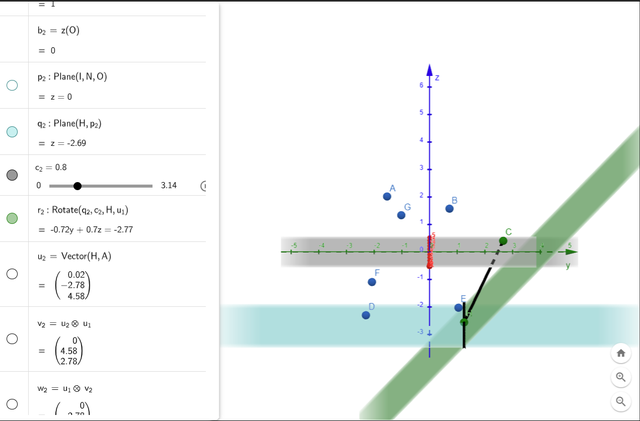
# third point
def find_next_point(p0, p1, p2):
min_angle = math.pi
dirVector = VectorI(p0, p1)
normalVector = CrossI(VectorI(p0, p2), dirVector)
bestP = None
for p in pts:
if p == p0 or p == p1 or p == p2:
continue
newVector = VectorI(p0, p)
angle = angle_about_axis(newVector, dirVector, normalVector)
if angle < min_angle:
min_angle = angle
bestP = p
return bestP
p2 = find_next_point(p0, p1, Invisible(p0 + xDir))
p2.color = "purple"
Segment(p0, p2)
Segment(p1, p2)
Polygon([p0, p1, p2])
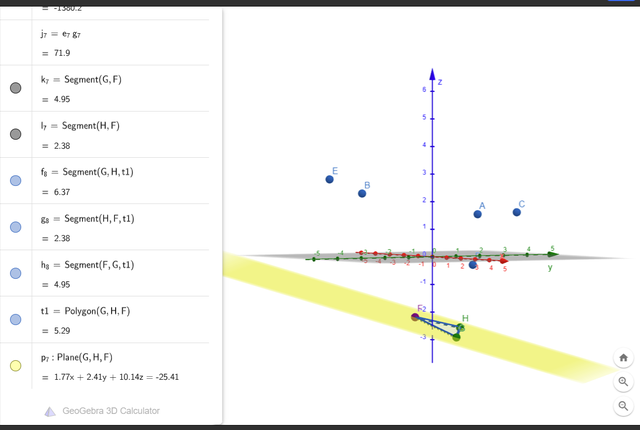
plane2 = Plane(p0, p1, p2, color = "yellow", is_visible = False)Дальше, перед переходом к финальной части — цикла построения следующих граней от известной, можно поиграться с ручным построением новых граней от ребёр построенной.
Поиск в ширину — построение 3х новых граней от каждого ребра гиперграни:
#4
p3 = find_next_point(p1, p0, p2)
Segment(p0, p3)
Segment(p1, p3)
Polygon([p0, p1, p3])
print(p3.caption)
#5
p4 = find_next_point(p0, p2, p1)
Segment(p2, p4)
Segment(p0, p4)
Polygon([p2, p0, p4])
print(p4.caption)
#6
p5 = find_next_point(p2, p1, p0)
Segment(p2, p5)
Segment(p1, p5)
Polygon([p2, p1, p5])
print(p5.caption)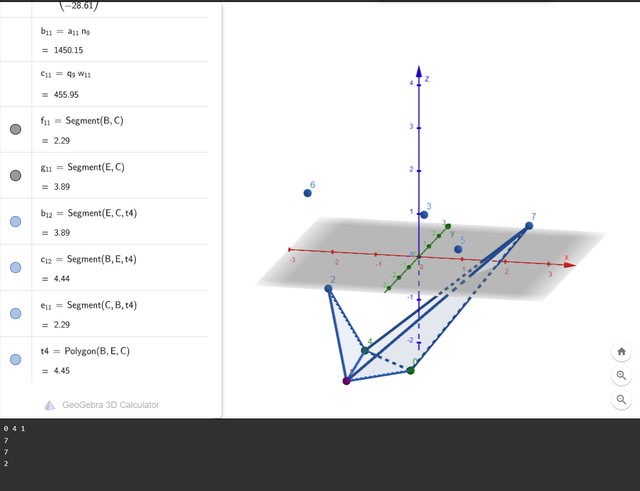
линк
От нижней грани “тянутся” три новых грани, охватывающие следующие части оболочки
Поиск в глубину — от одного из ребёр строится следующая грани, затем от одного из её новых ребёр вновь строится следующая:
p4 = find_next_point(p1, p3, p0)
Segment(p1, p4)
Segment(p3, p4)
Polygon([p1, p3, p4])
print(p4.caption)
p5 = find_next_point(p3, p4, p1)
Segment(p5, p3)
Segment(p5, p4)
Polygon([p5, p3, p4])
print(p5.caption)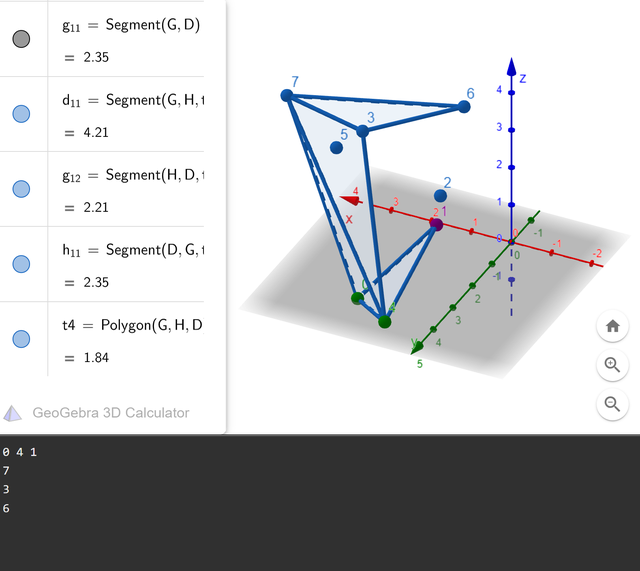
линк
Тут выглядит как “щупальце”, охватывающее одну из сторон.
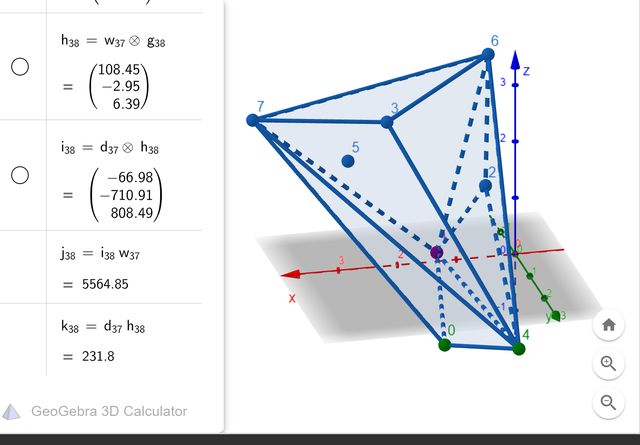
Для построения полной оболочки осталось добавить построение новых граней (поиском в ширину или глубину) до тех пор, пока не будут охвачены все точки оболочки. Идея описывалась в начале — для новой добавленной грани её два новых ребра добавляются в очередь/стек для раскрытия на следующих шагах, если для этого ребра ещё не были найдены обе содержащие его грани. Когда список ребёр для раскрытия заканчивается — оболочка готова!
faces = set()
faces.add(frozenset((p0, p1, p2)))
edge_queue = deque([
(p1, p0, p2),
(p0, p2, p1),
(p2, p1, p0),
])
step = 0
MAX_STEP = 99 # для отладки отдельных шагов
while edge_queue:
step += 1
if step > MAX_STEP:
break
a, b, c = edge_queue.popleft()
p = find_next_point(a, b, c)
if p is None:
continue # вырожденное ребро
face = frozenset((a, b, p))
if face in faces:
continue # уже есть такая грань
# добавляем новую грань
faces.add(face)
# отрисуем
Segment(a, p)
Segment(b, p)
Polygon([a, b, p])
print(p.caption)
# ставим в очередь её два новых ребра
edge_queue.append((p, b, a))
edge_queue.append((a, p, b))(если убрать random.seed(1) можно тестировать каждый раз на новых случайных данных)
Что хотелось бы прикрутить ещё:Geogebra на тысяче вспомогательных построений начинает подтормаживать, она всё-таки учебная программа на Java. Хотя скорее всего достаточно использовать удаление вспомогательных построений, как в прошлой посте, и прокинуть из js возможность отключать перестроение на каждом новом добавленном элементе, чтобы отсылать все команды одной пачкой